机器学习(ML)通常被定义为模仿智能人类能力的数据驱动技术,它从经验中一点一点地提升其准确性。它从收集大量数据开始,如数字、文本、图像等。在用数据进行训练后,ML算法建立了一个逻辑模型,通过尽可能少的人为干预来识别模式。在样本训练数据的帮助下,程序员在引入新的数据集之前测试模型的有效性。训练数据越多,预测效果越好
然而,如果训练数据集有偏见、不一致甚至错误,我们就不能指望对新数据进行可靠的模式或预测。但随着这一领域的快速扩展,我们可以通过强制执行一个始终遵循自然规律的物理框架来约束ML模型
在我们最近在《应用物理学杂志》上的工作中,我们开发了一个这样的物理约束ML模型,以深入了解金属氧化物半导体(MOS)电容器的静电学,这是当前CMOS(互补金属氧化物半导体)技术的基本组成部分
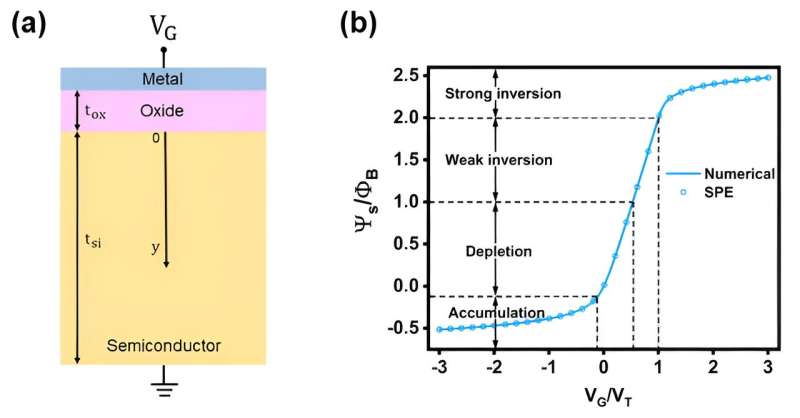
MOS电容器由掺杂的半导体本体、薄绝缘体(即氧化物)和称为栅极的金属电极组成。根据施加的栅极电压的值,它以三种模式工作:累积、耗尽和反转。在累积模式中,类似于掺杂剂类型的移动电荷载流子通过在氧化物-半导体界面处累积而形成薄层
随着栅极电压的增加,界面上的移动电荷逐渐耗尽,留下相反极性的不动离子。它在半导体表面产生一个不断扩大的电位降。随着栅极电压的进一步升高,在氧化物-半导体界面下方形成反向掺杂剂类型但浓度相似的移动电荷载流子层。因此,我们认为MOS电容器已进入反转模式
MOS电容器的静电由泊松-玻尔兹曼方程(PBE)控制,该方程是一个高度非线性的微分方程(DE)。DE表示一个或多个自变量的函数与其导数之间的相互关系。函数表示一个物理量,导数表示相对于自变量的变化率
最好在计算机上求解非线性DE,因为分析解通常很棘手。标准技术(例如,有限差分法、有限元法、射击法、样条曲线)和基于这些技术构建的用户友好的软件包可用于解决各种DE
神经网络(NNs)是最近出现的ML的一个子集,在几个科学和工程学科中产生了重大影响,它可以毫不费力地解决非线性DE。它们使用类似于人脑的分层结构中的互连节点,使生物神经元相互发出信号
NNs可以准确地逼近复杂的多元函数,并处理传统技术中的困难,例如有限元方法和样条函数中对离散化的依赖。神经网络的主要缺点是它们的训练速度慢,计算量大。然而,随着计算和优化技术的改进,我们战胜了这一挑战。在这里我们研究了机器是否可以通过使用ML求解PBE来学习MOS电容器的物理原理是非常通用的,可以用于处理任何DE,边界条件(BCs)在PINN中不受严格约束
相反,它们与DE一起作为惩罚组合到损失函数中,该函数计算ML模型中预测值和实际值之间的差。因此,它不能保证完全满足BCs。另一方面,Lagaris等人提出了另一种规避这一问题的技术
它使用控制方程来找到一个适合DE的试解。这种方法完全满足BC。然而,没有一般的程序来构建这样的试验解,特别是对于我们在MOS电容器的情况下面临的复杂边界条件
我们求解MOS电容器PBE的方法是由PINN和Lagaris等人的方法推动的。到目前为止,后一种方法已用于生成Neumann和Dirichlet BCs的试验,这相对简单。相比之下,我们的PBE需要涉及函数及其导数的简单Dirichlet BC和复杂Robin BC
尽管它具有高度非线性的性质,但我们表明,使用Lagaris等人的方法以满足PBE的两个BC的函数形式(即,以一个或多个函数为自变量的函数)构建试验解是具有挑战性的,但也是可能的。在我们的模型中,我们对设备的物理域进行了精确采样,以根据试验解构建损失函数
样本数量决定了计算损失函数和优化试验的复杂性。因此,我们构思了一种基于物理的采样方案,并将设备参数随机引入模型中。这种方法有助于模型获得非凡的精度
我们已经根据传统数字验证了我们的模型
We have validated our model against traditional numerical methods available in Python, as well as the industry-standard surface potential equation (SPE).
Through this study, we have found that our NN model can learn the relationship between input variables (i.e., thickness of the semiconductor, gate voltage, oxide thickness, and doping concentration) and the semiconductor potential.
Moreover, it is able to capture several relevant aspects of MOS device physics, such as the doping-dependent depletion width, variation of threshold voltage with oxide thickness and doping, and the low-frequency capacitance-voltage characteristics, in addition to interpreting the accumulation, depletion and inversion mechanisms. This model continues to obey device physics even outside the sampling domain.
In summary, for the first time, we report the possibility of an ML model to replicate the fundamental physics of MOS capacitors without using any labeled data (in contrast to typical supervised ML). We show that the commonly used PINN methodology fails to learn the Poisson-Boltzmann equation due to its dynamic nature posed by the unique boundary conditions.
We formulate a parametric model that naturally satisfies the boundary conditions so that the expressive power of neural networks can be harnessed to secure solutions with exceptional accuracy. In addition, we show that the proposed model can accurately capture critical insights such as depletion width, threshold voltage, inversion charge, etc.
This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.



